基本概念

f (x) 满足 1°[a,b]上连续 2°(a,b)内可导 3°f (a)=f(b) ，则至少∃ξ∈(a,b)，使得f'(ξ)=0.

Note：

1. 当证明"f(ξ)=0"形式的等式时，若左侧连续，优先考虑介值定理，若左侧连续性未知，优先考虑罗尔定理.

2. 辅助函数的构造一般有3种方法：1°猜 2°不定积分 3°微分方程

3. 找2个相等点是关键

1.辅助函数的构造

①基本构造

②“缺非0因子”

原理：F‘(x)|x=ξ=0 因式分解 为f(ξ)∙g(ξ)=0

若g(ξ)≠0 证f(ξ)=0

Note：

命题老师都是坏坏的.他就故意省去恒不为零的f(ξ)，让你自己用注意力主动补上f(ξ).

③缺项

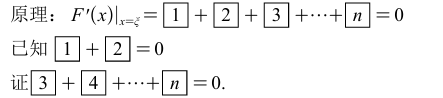
2.找不同的两个点

①用介值定理找

②用中值定理找

罗尔中值定理

拉格朗日中值定理

积分中值定理

3.两个变化

1°1次（多次）罗尔定理

2° 费马定理